源链接:https://www.coursera.org/learn/neural-networks-deep-learning/ Week4 assignment(part 1 of 2)
- 这周内容:实现所有建立深度神经网络需要的函数
- 下周内容:构建用于图像分类的深度神经网络
本次作业的要求是
- 用非线性单元(如:ReLU)来改进模型
- 建立深度神经网络
- 实现易于实用的神经网络
符号标记
- 上标 $[l]$ 表示与第$l$层相关的量
- 例:$a^{[L]}$是第$L$层激活层,$W^{[L]}$和$b^{[L]}$分别是第$L$层的参数。
- 上标$(i)$表示与第$i$个样本相关的量
- 例:$x^(i)$是第$i$个训练样本
- 下标$i$表示某个向量的第$i$个量
- 例:$a^{[l]}_i$表示第$l$个激活层的第$i$个元素
Packages
首先导入你需要用到的所有python库。
numpymatplotlibdnn_utils:提供了本文需要用到的一些必要的函数testCases:提供了一些测试实例np.random.seed(1)用来保证所有的随机函数都是一致的。
|
|
Outline of the Assignment
- 初始化两层神经网络和$L$层神经网络的参数
- 实现前向传播模块(forward propagation module)
- 实现某一层前向传播的线性部分(LINEAR)(结果为$Z^{[l]}$)
- 给定激活函数ACTIVATION(relu/sigmoid)
- 结合前两步实现新的[LINEAR->ACTIVATION]前向函数
- 堆叠[LINEAR->ACTIVATION]前向函数$L-1$次(从第1层到第$L-1$层,在结尾加上[LINEAR->SIGMOID]作为最后第$L$层),则得到新的函数 L_model_forward。
- 计算损失
- 实现后向传播模块
- 计算某一层后向传播的线性部分LINEAR。
- 给定激活函数ACTIVATION的梯度(relu_backward/sigmoid_backward)。
- 结合前面两步得到新的后向函数[LINEAR->ACTIVATION]。
- 堆叠[LINEAR->ACTIVATION]后向函数$L-1$次,并加入[LINEAR->SIGMOID]后向函数,得到新的函数 L_model_backward。
- 最后更新参数。
Initialization
下文实现了两个初始化的函数,第一个是用来初始化两层神经网络,第二个是$L$层神经网络。
2-lay Neural Network
Exercise: 创建并初始化二层神经网络
Instructions:
- 模型结构是LINEAR->RELU->LINEAR->SIGMOID
- 权重矩阵随机初始化,用:
np.random.randn(shape)*0.01 - 偏差初始化为0:
mp.zeros(shape)
|
|
|
|
Expected output:
| name | value |
|---|---|
| W1 | [[ 0.01624345 -0.00611756] [-0.00528172 -0.01072969]] |
| W2 | [[ 0.00865408 -0.02301539]] |
| b1 | [[ 0.] [ 0.]] |
| b2 | [[ 0.]] |
L-layer Neural Network
L层神经网络的初始化要相对复杂一些。初始化的时候要注意匹配每一层的维度,$n^{[l]}$表示第$l$层的神经元数量,如果输入$X$是$(12288,209)$(有209个训练样本),则:
| shape of W | shape of b | Activation | Shape of Activation | |
|---|---|---|---|---|
| Layer1 | $(n^{[1]},12288)$ | $(n^{[1]},1)$ | $Z^{[1]}=W^{[1]}X+b^{[1]}$ | $(n^{[1]},209)$ |
| Layer2 | $(n^{[2]},n^{[1]})$ | $(n^{[2]},1)$ | $Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]}$ | $(n^{[2]},209)$ |
| … | … | … | … | … |
| Layer L-1 | $(n^{[L-1]},n^{[L-2]})$ | $(n^{[L-1]},1)$ | $Z^{[L-1]}=W^{[L-1]}A^{[L-2]}+b^{[L-1]}$ | $(n^{[L-1]},209)$ |
| Layer L | $(n^{[L]},n^{[L-1]})$ | $(n^{[L]},1)$ | $Z^{[L]}=W^{[L]}A^{[L-1]}+b^{[L]}$ | $(n^{[L]},209)$ |
需要注意的是,由于python的broadcast特性,如果计算 WX+b,最后得到的结果是:
$$W = \begin{bmatrix} j & k & l \\ m & n & o \\ p & q & r \end{bmatrix},
X = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix},
b = \begin{bmatrix} s \\ t \\ u \end{bmatrix}$$
$$WX+b = \begin{bmatrix} (ja+kd+lg)+s & (jb+ke+lh)+s & (jc+kf+li)+s \\
(ma+nd+og)+t & (mb+ne+oh)+t & (mc+nf+oi)+t \\
(pa+qd+rg)+u & (pb+qe+rh)+u & (pc+qf+ri)+u\end{bmatrix}$$
Excercise 实现L层神经网络的初始化
Instructions:
- 模型结构是[LINEAR->RELU] × (L-1)->LINEAR->SIGMOID. 由L-1层RELU激活函数和带有sigmoid函数的输出层构成。
- 权重矩阵随机初始化,采用
np.random.rand(shape)*0.01 - 偏差向量零初始化,采用
np.zeros(shape) - 神经网络不同层的单元数储存在变量
layer_dims中,例如,如果layer_dims的值为[2,4,1],则神经网络输入神经元有2个,隐层有4个神经元,输出层有1个神经元,也意味着W1的维度为(4,2),b1为(4,1),W2为(1,4),b2为(1,1)。
|
|
|
|
Expected output:
| name | value |
|---|---|
| W1 | [[ 0.01788628 0.0043651 0.00096497 -0.01863493 -0.00277388] [-0.00354759 -0.00082741 -0.00627001 -0.00043818 -0.00477218] [-0.01313865 0.00884622 0.00881318 0.01709573 0.00050034] [-0.00404677 -0.0054536 -0.01546477 0.00982367 -0.01101068]] |
| b1 | [[ 0.] [ 0.] [ 0.] [ 0.]] |
| W2 | [[-0.01185047 -0.0020565 0.01486148 0.00236716] [-0.01023785 -0.00712993 0.00625245 -0.00160513] [-0.00768836 -0.00230031 0.00745056 0.01976111]] |
| b2 | [[ 0.] [ 0.] [ 0.]] |
Forward propagation module
Linear Forward
本模块按顺序实现了一下函数:
- LINEAR
- LINEAR->ACTIVATION,其中激活函数是ReLU或者Sigmoid
- [LINEAR->RELU] × (L-1) -> LINEAR -> SIGMOID
线性前向模块主要实现如下公式:
$$Z^{[l]} = W^{[l]}A^{[l-1]}+b^{[l]}$$
其中$A^{[0]}=X$
Excersice: 实现前向传播的线性部分
|
|
|
|
Linear-Activation Forward
本文将会用到两种激活函数:
- Sigmoid: $\sigma(Z)=\sigma(WA+b)=\frac{1}{1+e^{-(WA+b)}}$,这个函数返回两项值:激活后的值’a’和包含’Z’的’cache’。调用方法为:
A, activation_cache = sigmoid(Z) - ReLU:ReLU函数的数学形式是 $A=RELU(Z)=\max(0,Z)$,这个函数返回两项值:激活后的值’a’和包含’Z’的’cache’。调用方法为:
A, activation_cache = relu(Z)
Excersice: 实现前向传播中的LINEAR->ACTIVATION层,即$A^{[l]}=g(Z^{[l]})=g(W^{[l]}A^{[l-1]}+b^{[l]})$,其中’g’可以是sigmoid()或者relu()。用linear_forward()和对应的激活函数。
|
|
|
|
L-layer model
对于有L层的神经网络来说,前向传播由L-1个linear_activation_forwardwith RELU和一个linear_activation_forwardwith SIGMOID构成。
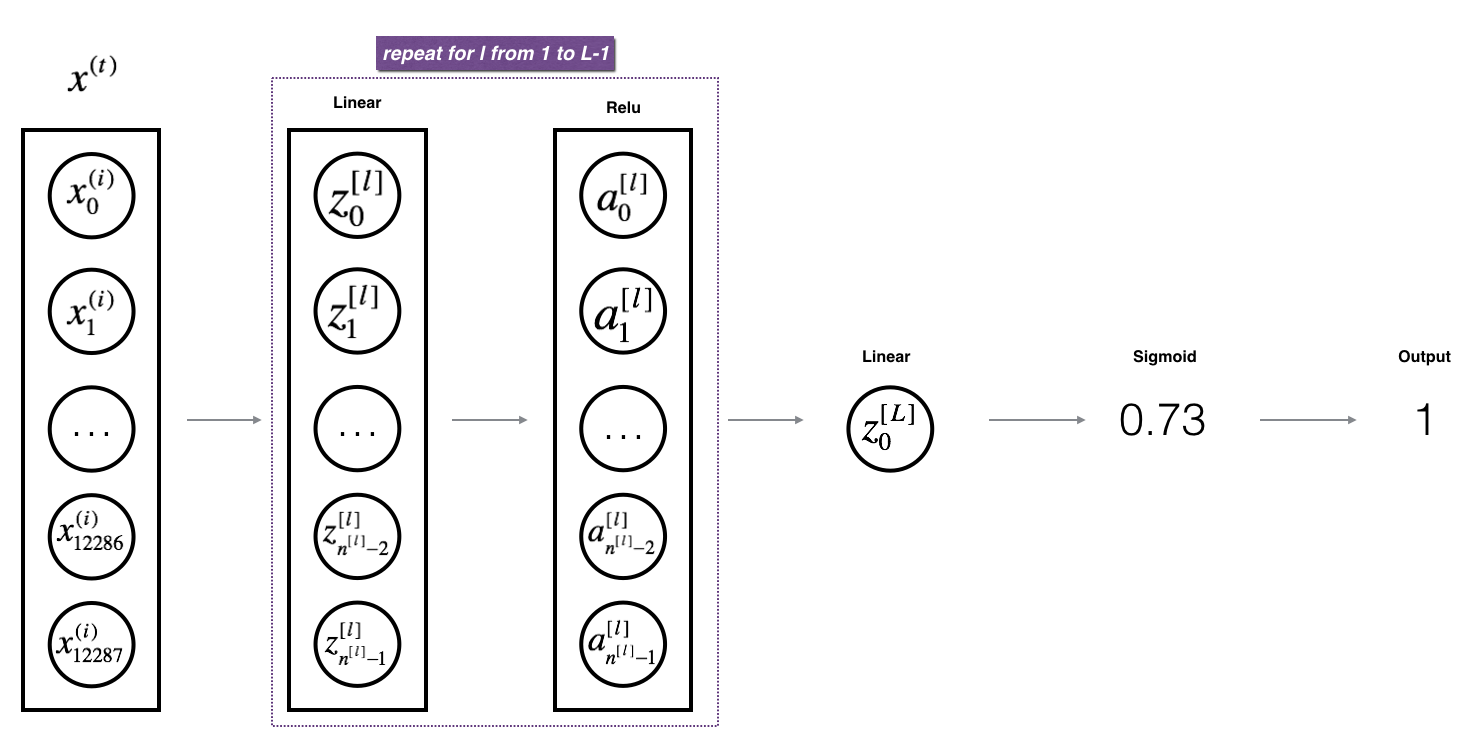
Excersice:实现上述模型的前向传播
|
|
|
|
Cost function
Excersice:计算交叉熵损失(cross-entropy cost)$J$,公式如下:
$$-\frac{1}{m} \sum\limits_{i = 1}^{m} (y^{(i)}\log\left(a^{[L] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[L] (i)}\right))$$
|
|
|
|
Backward propagation module
Reminder: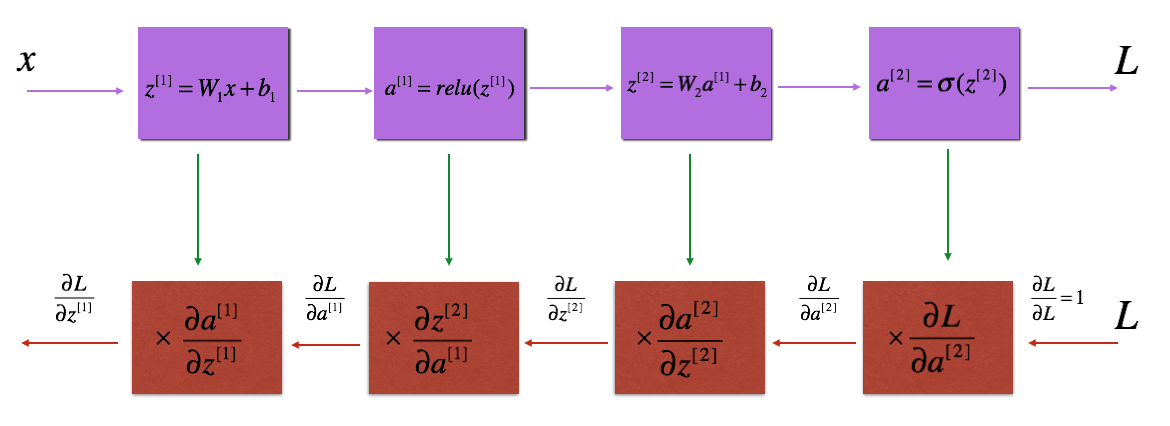
与前向传播类似,后向传播的实现也分成三个步骤:
- LINEAR backward
- LINEAR->ACTIVATION backward,其中ACTIVATION是ReLU或者sigmoid函数
- [LINEAR->RELU]× (L-1)->LINEAR->SIGMOID backward
Linear backward
对于第l层神经网络,线性部分是:$Z^{[l]} = W^{[l]}A^{[l-1]}+b^{[l]}$。假设已知$d Z^{[l]} = \frac{\partial L}{\partial Z^{[l]}}$,需要求的是 $dW^{[l]}$, $db^{[l]}$以及$dA^{[l-1]}$。
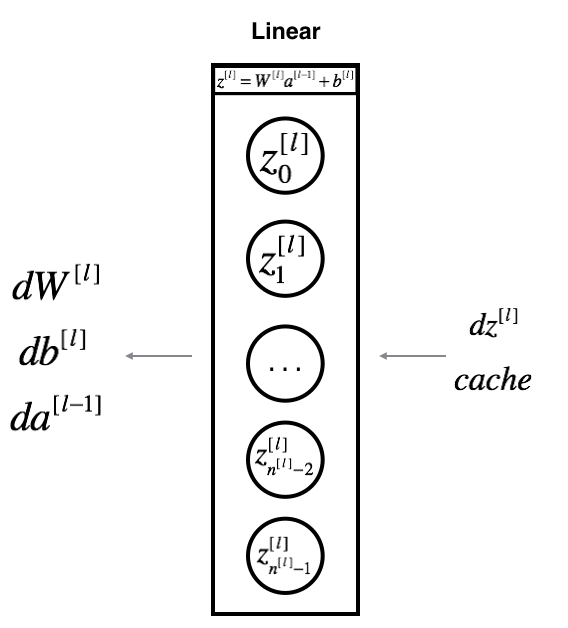
三个输出$dW^{[l]}$, $db^{[l]}$以及$dA^{[l-1]}$可以用输入$d Z^{[l]}$ 来计算:
$$dW^{[l]}=\frac{\partial L}{\partial W^{[l]}} = \frac{1}{m}d Z^{[l]}A^{[l-1]T}$$
$$ db^{[l]}=\frac{\partial L}{\partial b^{[l]}} = \frac{1}{m} \sum^m_{i=1}dZ^{[l] (i)} $$
$$dA^{[l-1]} = \frac{\partial L}{\partial A^{[l-1]}} = W^{[l]T}dZ^{[l]}$$
|
|
|
|
Linear-Activation backward
sigmoid_backward 实现了SIGMOID函数的后向传播,调用方法:
dZ = sigmoid_backward(dA, activation_cache)relu_backward 实现了relu函数的后向传播,调用方法:
dZ = relu_backward(dA, activation_cache)
如果$g(.)$是激活函数,sigmoid_backward和relu_backward的计算是:
$$dZ^{[l]} = dA^{[l]}*g’(Z^{[l]})$$
Excersice:实现LINEAR->ACTIVATION层的后向传播:
|
|
|
|
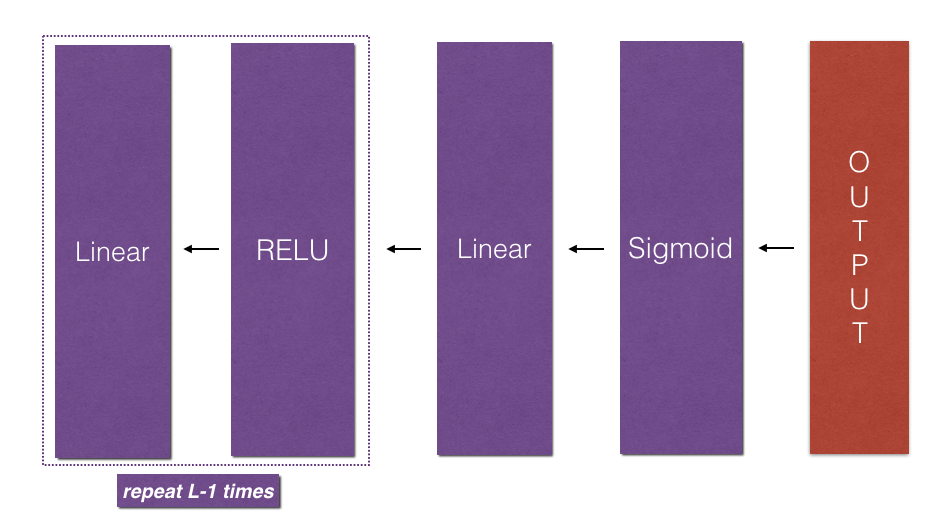
L-Model backward
当实现L_model_forward函数时,在每次迭代中都保存了(X,W,b,Z)的值,在后向传播模块中,你将用到这些值来计算梯度。
Initializing backpropagation: 上述网络的输出是:$A^{[L]} = \sigma(Z^{[L]})$。因此需要计算$dAL = \frac{\partial L}{\partial A^{[L]}}$.
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
Excercise:实现后向传播:[LINEAR->RELU] × (l-1) -> LINEAR -> SIGMOID 模型。
|
|
|
|
Update parameters
在这一节,你将用梯度下降法更新模型参数:
$$b^{[l]} = b^{[l]} - \alpha db^{[l]}$$
其中$\alpha$是学习率。
Excercise:实现update_parameters()函数
|
|
|
|